面試精選:鏈表問題集錦
鏈表問題在面試過程中也是很重要也很基礎的一部分,鏈表本身很靈活,很考查編程功底,所以是很值得考的地方。我將複習過程中覺得比較好的鏈表問題整理了下。
下面是本文所要用到鏈表節點的定義:
struct Node{
int data;
Node* next;
};
1. 在O(1)時間刪除鏈表節點
題目描述:給定鏈表的頭指針和一個節點指針,在O(1)時間刪除該節點。[Google面試題]
分析:本題與《編程之美》上的「從無頭單鏈表中刪除節點」類似。主要思想都是「狸貓換太子」,即用下一個節點數據覆蓋要刪除的節點,然後刪除下一個節點。但是如果節點是尾節點時,該方法就行不通了。
代碼如下:
//O(1)時間刪除鏈表節點,從無頭單鏈表中刪除節點
void deleteRandomNode(Node *cur)
{
assert(cur != NULL);
assert(cur->next != NULL); //不能是尾節點
Node* pNext = cur->next;
cur->data = pNext->data;
cur->next = pNext->next;
delete pNext;
}
2. 單鏈表的轉置
題目描述:輸入一個單向鏈表,輸出逆序反轉後的鏈表
分析:鏈表的轉置是一個很常見、很基礎的數據結構題了,非遞歸的算法很簡單,用三個臨時指針 pre、head、next 在鏈表上循環一遍即可。遞歸算法也是比較簡單的,但是如果思路不清晰估計一時半會兒也寫不出來吧。
下面是循環版本和遞歸版本的鏈表轉置代碼:
//單鏈表的轉置,循環方法
Node* reverseByLoop(Node *head)
{
if(head == NULL || head->next == NULL)
return head;
Node *pre = NULL;
Node *next = NULL;
while(head != NULL)
{
next = head->next;
head->next = pre;
pre = head;
head = next;
}
return pre;
}
//單鏈表的轉置,遞歸方法
Node* reverseByRecursion(Node *head)
{
//第一個條件是判斷異常,第二個條件是結束判斷
if(head == NULL || head->next == NULL)
return head;
Node *newHead = reverseByRecursion(head->next);
head->next->next = head;
head->next = NULL;
return newHead; //返回新鏈表的頭指針
}
3. 求鏈表倒數第k個節點
題目描述:輸入一個單向鏈表,輸出該鏈表中倒數第k個節點,鏈表的倒數第0個節點為鏈表的尾指針。
分析:設置兩個指針 p1、p2,首先 p1 和 p2 都指向 head,然後 p2 向前走 k 步,這樣 p1 和 p2 之間就間隔 k 個節點,最後 p1 和 p2 同時向前移動,直至 p2 走到鏈表末尾。
代碼如下:
//倒數第k個節點
Node* theKthNode(Node *head,int k)
{
if(k < 0) return NULL; //異常判斷
Node *slow,*fast;
slow = fast = head;
int i = k;
for(;i>0 && fast!=NULL;i--)
{
fast = fast->next;
}
if(i > 0) return NULL; //考慮k大於鏈表長度的case
while(fast != NULL)
{
slow = slow->next;
fast = fast->next;
}
return slow;
}
4. 求鏈表的中間節點
題目描述:求鏈表的中間節點,如果鏈表的長度為偶數,返回中間兩個節點的任意一個,若為奇數,則返回中間節點。
分析:此題的解決思路和第3題「求鏈表的倒數第 k 個節點」很相似。可以先求鏈表的長度,然後計算出中間節點所在鏈表順序的位置。但是如果要求只能掃瞄一遍鏈表,如何解決呢?最高效的解法和第3題一樣,通過兩個指針來完成。用兩個指針從鏈表頭節點開始,一個指針每次向後移動兩步,一個每次移動一步,直到快指針移到到尾節點,那麼慢指針即是所求。
代碼如下:
//求鏈表的中間節點
Node* theMiddleNode(Node *head)
{
if(head == NULL)
return NULL;
Node *slow,*fast;
slow = fast = head;
//如果要求在鏈表長度為偶數的情況下,返回中間兩個節點的第一個,可以用下面的循環條件
//while(fast && fast->next != NULL && fast->next->next != NULL)
while(fast != NULL && fast->next != NULL)
{
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
5. 判斷單鏈表是否存在環
題目描述:輸入一個單向鏈表,判斷鏈表是否有環?
分析:通過兩個指針,分別從鏈表的頭節點出發,一個每次向後移動一步,另一個移動兩步,兩個指針移動速度不一樣,如果存在環,那麼兩個指針一定會在環裡相遇。
代碼如下:
//判斷單鏈表是否存在環,參數circleNode是環內節點,後面的題目會用到
bool hasCircle(Node *head,Node *&circleNode)
{
Node *slow,*fast;
slow = fast = head;
while(fast != NULL && fast->next != NULL)
{
fast = fast->next->next;
slow = slow->next;
if(fast == slow)
{
circleNode = fast;
return true;
}
}
return false;
}
6. 找到環的入口點
題目描述:輸入一個單向鏈表,判斷鏈表是否有環。如果鏈表存在環,如何找到環的入口點?
解題思路: 由上題可知,按照 p2 每次兩步,p1 每次一步的方式走,發現 p2 和 p1 重合,確定了單向鏈表有環路了。接下來,讓p2回到鏈表的頭部,重新走,每次步長不是走2了,而是走1,那麼當 p1 和 p2 再次相遇的時候,就是環路的入口了。
為什麼?:假定起點到環入口點的距離為 a,p1 和 p2 的相交點M與環入口點的距離為b,環路的周長為L,當 p1 和 p2 第一次相遇的時候,假定 p1 走了 n 步。那麼有:
p1走的路徑: a+b = n; p2走的路徑: a+b+kL = 2n; p2 比 p1 多走了k圈環路,總路程是p1的2倍
根據上述公式可以得到 k*L=a+b=n顯然,如果從相遇點M開始,p1 再走 n 步的話,還可以再回到相遇點,同時p2從頭開始走的話,經過n步,也會達到相遇點M。
顯然在這個步驟當中 p1 和 p2 只有前 a 步走的路徑不同,所以當 p1 和 p2 再次重合的時候,必然是在鏈表的環路入口點上。
代碼如下:
//找到環的入口點
Node* findLoopPort(Node *head)
{
//如果head為空,或者為單結點,則不存在環
if(head == NULL || head->next == NULL) return NULL;
Node *slow,*fast;
slow = fast = head;
//先判斷是否存在環
while(fast != NULL && fast->next != NULL)
{
fast = fast->next->next;
slow = slow->next;
if(fast == slow)
break;
}
if(fast != slow) return NULL; //不存在環
fast = head; //快指針從頭開始走,步長變為1
while(fast != slow) //兩者相遇即為入口點
{
fast = fast->next;
slow = slow->next;
}
return fast;
}
7. 編程判斷兩個鏈表是否相交
題目描述:給出兩個單向鏈表的頭指針(如下圖所示),
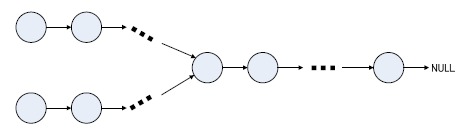
比如h1、h2,判斷這兩個鏈表是否相交。這裡為了簡化問題,我們假設兩個鏈表均不帶環。
解題思路:
直接循環判斷第一個鏈表的每個節點是否在第二個鏈表中。但,這種方法的時間複雜度為O(Length(h1) * Length(h2))。顯然,我們得找到一種更為有效的方法,至少不能是O(N^2)的複雜度。
針對第一個鏈表直接構造hash表,然後查詢hash表,判斷第二個鏈表的每個節點是否在hash表出現,如果所有的第二個鏈表的節點都能在hash表中找到,即說明第二個鏈表與第一個鏈表有相同的節點。時間複雜度為為線性:O(Length(h1) + Length(h2)),同時為了存儲第一個鏈表的所有節點,空間複雜度為O(Length(h1))。是否還有更好的方法呢,既能夠以線性時間複雜度解決問題,又能減少存儲空間?
轉換為環的問題。把第二個鏈表接在第一個鏈表後面,如果得到的鏈表有環,則說明兩個鏈表相交。如何判斷有環的問題上面已經討論過了,但這裡有更簡單的方法。因為如果有環,則第二個鏈表的表頭一定也在環上,即第二個鏈表會構成一個循環鏈表,我們只需要遍歷第二個鏈表,看是否會回到起始點就可以判斷出來。這個方法的時間複雜度是線性的,空間是常熟。
進一步考慮「如果兩個沒有環的鏈表相交於某一節點,那麼在這個節點之後的所有節點都是兩個鏈表共有的」這個特點,我們可以知道,如果它們相交,則最後一個節點一定是共有的。而我們很容易能得到鏈表的最後一個節點,所以這成了我們簡化解法的一個主要突破口。那麼,我們只要判斷兩個鏈表的尾指針是否相等。相等,則鏈表相交;否則,鏈表不相交。 所以,先遍歷第一個鏈表,記住最後一個節點。然後遍歷第二個鏈表,到最後一個節點時和第一個鏈表的最後一個節點做比較,如果相同,則相交,否則,不相交。這樣我們就得到了一個時間複雜度,它為O((Length(h1) + Length(h2)),而且只用了一個額外的指針來存儲最後一個節點。這個方法時間複雜度為線性O(N),空間複雜度為O(1),顯然比解法三更勝一籌。
解法四的代碼如下:
//判斷兩個鏈表是否相交
bool isIntersect(Node *h1,Node *h2)
{
if(h1 == NULL || h2 == NULL) return false; //異常判斷
while(h1->next != NULL)
{
h1 = h1->next;
}
while(h2->next != NULL)
{
h2 = h2->next;
}
if(h1 == h2) return true; //尾節點是否相同
else return false;
}
8. 擴展:鏈表有環,如何判斷相交
題目描述:上面的問題都是針對鏈表無環的,那麼如果現在,鏈表是有環的呢?上面的方法還同樣有效麼?
分析:如果有環且兩個鏈表相交,則兩個鏈表都有共同一個環,即環上的任意一個節點都存在於兩個鏈表上。因此,就可以判斷一鏈表上倆指針相遇的那個節點,在不在另一條鏈表上。
代碼如下:
//判斷兩個帶環鏈表是否相交
bool isIntersectWithLoop(Node *h1,Node *h2)
{
Node *circleNode1,*circleNode2;
if(!hasCircle(h1,circleNode1)) //判斷鏈錶帶不帶環,並保存環內節點
return false; //不帶環,異常退出
if(!hasCircle(h2,circleNode2))
return false;
Node *temp = circleNode2->next;
while(temp != circleNode2)
{
if(temp == circleNode1)
return true;
temp = temp->next;
}
return false;
}
9. 擴展:兩鏈表相交的第一個公共節點
題目描述:如果兩個無環單鏈表相交,怎麼求出他們相交的第一個節點呢?
分析:採用對齊的思想。計算兩個鏈表的長度 L1 , L2,分別用兩個指針 p1 , p2 指向兩個鏈表的頭,然後將較長鏈表的 p1(假設為 p1)向後移動L2 - L1個節點,然後再同時向後移動p1 , p2,直到 p1 = p2。相遇的點就是相交的第一個節點。
代碼如下:
//求兩鏈表相交的第一個公共節點
Node* findIntersectNode(Node *h1,Node *h2)
{
int len1 = listLength(h1); //求鏈表長度
int len2 = listLength(h2);
//對齊兩個鏈表
if(len1 > len2)
{
for(int i=0;i<len1-len2;i++)
h1=h1->next;
}
else
{
for(int i=0;i<len2-len1;i++)
h2=h2->next;
}
while(h1 != NULL)
{
if(h1 == h2)
return h1;
h1 = h1->next;
h2 = h2->next;
}
return NULL;
}
10. 總結
可以發現,在鏈表的問題中,通過兩個的指針來提高效率是很值得考慮的一個解決方案,所以一定要記住這種解題思路。記住幾種典型的鏈表問題解決方案,很多類似的題目都可以轉換到熟悉的問題再解決。
參考文獻
- 程序員編程藝術:第九章、閒話鏈表追趕問題
- 判斷單鏈表是否存在環,判斷兩個鏈表是否相交問題詳解
- 面試算法之鏈表操作集錦