OpenGL Angles to Axes

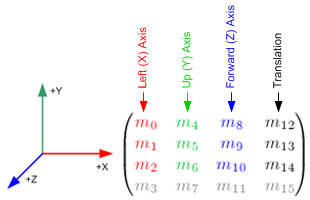
Left, Up and Forward Axis of OpenGL Matrix

The rotation angles directly affects the first 3 columns of OpenGL GL_MODELVIEW matrix, precisely left, up and forward axis elements. For example, if a unit vector along X axis, (1, 0, 0) is multiplied by an arbitrary 3x3 rotation matrix, then the result of the vector after rotation is;

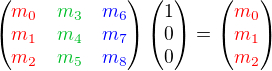
It means the first column (m₀, m₁, m₂) of the rotation matrix represents the coordinates of the left axis after rotated. Similarly, the second column is the up axis and the third column is the forward axis.

This article describes how to contruct GL_MODELVIEW matrix with rotation angles.

Axis Rotations

First, we look at a rotation around each axis; +X, +Y and +Z. We project three axes onto a plane in 3 different ways, so the axis that we want to rotate is facing toward you. The positive rotation direction becomes counter clockwise (right hand rule).

Rotation about Left(X) Axis (Pitch)

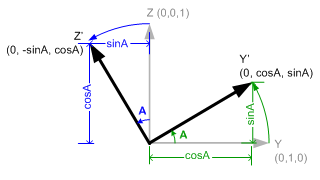
Rotation about Left(X) Axis

Initial value of up(Y) and forward(Z) axes are (0, 1, 0) and (0, 0, 1). If left(X) axis rotates A degree, then new up(Y') axis becomes (0, cosA, sinA) and forward(Z') becomes (0, -sinA, cosA). The new axes are inserted as column components of the 3x3 rotation matrix. Then, the rotation matrix becomes;

Rotation about Up(Y) Axis (Yaw, Heading)

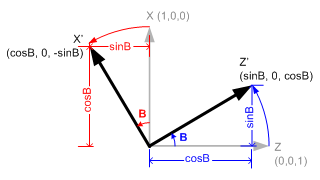
Rotation about Up(Y) Axis

Now, we rotate around up vector, which is facing toward you, with B angle . Left(X) axis is transformed from (1, 0, 0) to X' (cosB, 0, -sinB). And forward(Z) axis is from (0, 0, 1) to Z' (sinB, 0, cosB).

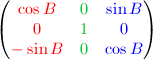
Rotation about Forward(Z) Axis (Roll)

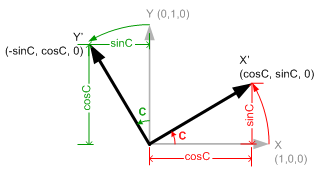
Rotation about Forward(Z) Axis

If we rotate forward(Z) axis with angle C degree, the original left(X) (1, 0, 0) axis becomes X' (cosC, sinC, 0), and up(Y) (0, 1, 0) axis becomes Y' (-sinC, cosC, 0).

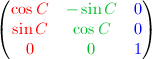
Angles To Axes

We can combine these separate axis rotations into one matrix by multiplying above 3 matrices together. Note that multiplication of matrices is not commutative, so a different order of matrix multiplication results in a different outcome. There are 6 different combinations are possible; R_xR_yR_z, R_xR_zR_y, R_yR_xR_z, R_yR_zR_x, R_zR_xR_y and R_zR_yR_x.

The left column of the combined rotation matrix is the left axis after rotated, the middle column is the up axis, and the right column is the forward axis.

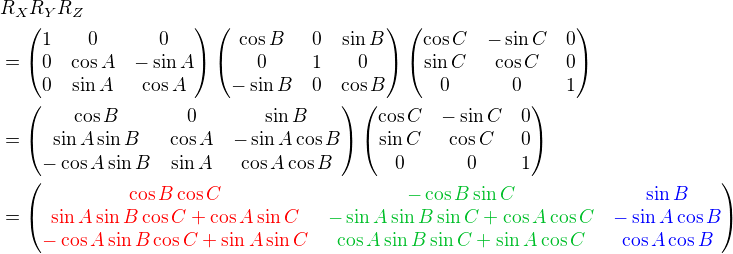
Rotation Matrix, RxRyRz

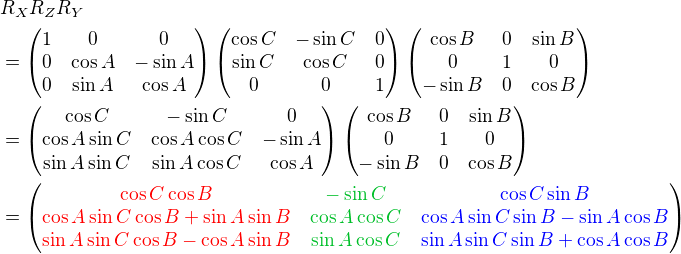
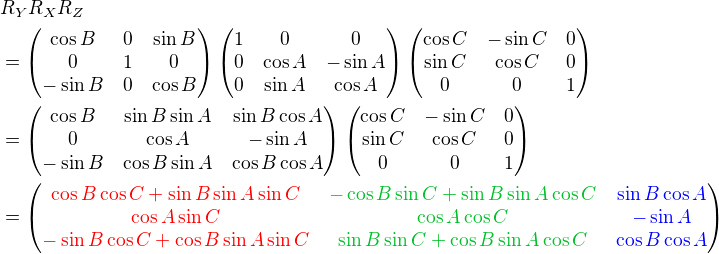
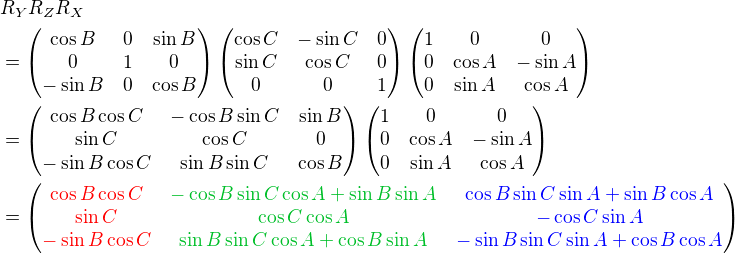
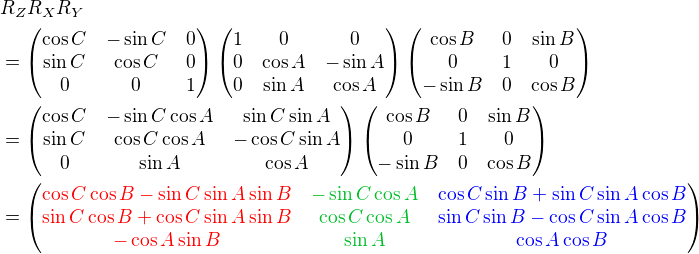
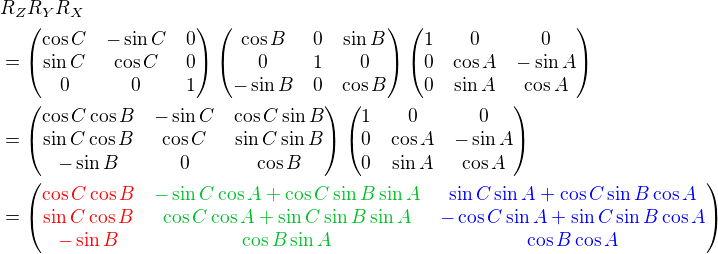
Here is a C++ example code for R_xR_yR_z combination. It performs 3 rotations in order of R_z (roll), R_y (yaw) then R_x (pitch). The results of left, up and forward axis can be used to construct GL_MODELVIEW matrix.

struct Vector3
{
    float x;
    float y;
    float z;
    Vector3() : x(0), y(0), z(0) {}; <span class="comment">// initialze when created</span>
};


<span class="comment">///////////////////////////////////////////////////////////////////////////////
// convert Euler angles(x,y,z) to axes(left, up, forward)
// Each column of the rotation matrix represents left, up and forward axis.
// The order of rotation is Roll-&gt;Yaw-&gt;Pitch (Rx*Ry*Rz)
// Rx: rotation about X-axis, pitch
// Ry: rotation about Y-axis, yaw(heading)
// Rz: rotation about Z-axis, roll
//    Rx           Ry          Rz
// |1  0   0| | Cy  0 Sy| |Cz -Sz 0|   | CyCz        -CySz         Sy  |
// |0 Cx -Sx|*|  0  1  0|*|Sz  Cz 0| = | SxSyCz+CxSz -SxSySz+CxCz -SxCy|
// |0 Sx  Cx| |-Sy  0 Cy| | 0   0 1|   |-CxSyCz+SxSz  CxSySz+SxCz  CxCy|
///////////////////////////////////////////////////////////////////////////////</span>
void anglesToAxes(const Vector3 angles, Vector3&amp; left, Vector3&amp; up, Vector3&amp; forward)
{
    const float DEG2RAD = 3.141593f / 180;
    float sx, sy, sz, cx, cy, cz, theta;

    <span class="comment">// rotation angle about X-axis (pitch)</span>
    theta = angles.x * DEG2RAD;
    sx = sinf(theta);
    cx = cosf(theta);

    <span class="comment">// rotation angle about Y-axis (yaw)</span>
    theta = angles.y * DEG2RAD;
    sy = sinf(theta);
    cy = cosf(theta);

    <span class="comment">// rotation angle about Z-axis (roll)</span>
    theta = angles.z * DEG2RAD;
    sz = sinf(theta);
    cz = cosf(theta);

    <span class="comment">// determine left axis</span>
    left.x = cy*cz;
    left.y = sx*sy*cz + cx*sz;
    left.z = -cx*sy*cz + sx*sz;

    <span class="comment">// determine up axis</span>
    up.x = -cy*sz;
    up.y = -sx*sy*sz + cx*cz;
    up.z = cx*sy*sz + sx*cz;

    <span class="comment">// determine forward axis</span>
    forward.x = sy;
    forward.y = -sx*cy;
    forward.z = cx*cy;
}